AC7. Planet-Star Systems

Chapter 7
We wonder “Where did we come from, in the big scheme of things?” That leads to questions of how our planet began, which in turn leads to the question, “Where did our Solar System come from?” and “Where did the Universe come from?” That last question will be a focus of the last chapter in this book, but the first question is one that some people have been struggling with for a long time and is the subject of Part I of this chapter.

But first… some Moon activities
Here are some activities from the Night Sky Network / Astronomical Society of the Pacific about the Sun-Earth-Moon system:
- Why Does the Moon Have Phases?
- Does the Moon Rotate?
- Skywatcher’s Guide to the Moon
- Spotting Craters
- Why Do Eclipses Happen?
Also, visit the SVS Moon Phase and Libration page to see the Moon at any hour of the year, play animations, and read detailed explanations. Every year since 2011, the NASA’s Science Visualization Studio (SVS) produces its annual visualization of the Moon’s phase and libration comprising 8760 hourly renderings of the precise size, orientation, and illumination of our nearest neighbor in space.
If you have a chance to view a partial eclipse of the Sun (when the Moon obscures part of the Sun), of course you must use a proper Sun filter for eye protection. See the American Astronomical Society web page on safe ways to view solar eclipses.
I. Evolution of Solar System Models
People in ancient civilizations observed the heavens with care and came to a number of conclusions that were excellent in explaining what they saw in terms of movement of the Sun, Moon, planets and stars. Babylonian astronomer-astrologers (Chaldeans) kept thorough clay-tablet records of eclipse observations covering many centuries, as long ago as 26 February 747 BC. They also knew that the lengths of the seasons are not equal. All early models of the Universe, based on obvious movements of things in the sky appearing to move around Earth, placed Earth at the very center of the Universe.

Hipparchus, a Greek astronomer, geographer, and mathematician that lived between 147 BC and 127 BC used Chaldean records to develop good models for the motion of the Sun, Moon, and planets that predicted positions used by sailors for navigation. He was the first to compile a trigonometric table, which he used in devising solar and lunar theories that could reliably predict solar eclipses. He measured the differences in the length of the seasons through equinox and solstice observations, finding that spring lasted 94.5 days (spring equinox to summer solstice), and summer lasted 92.5 days (from summer solstice to autumn equinox). That was an unexpected result since the prevailing idea was that the Sun moves around the Earth in a circle at a constant speed. Hipparchus’ solution was to place the Earth not at the center of the Sun’s motion, but at some distance from the center— about 1/24 of the radius of the orbit. That model described the apparent motion of the Sun fairly well.
Hipparchus created a star chart with about 850 stars and is perhaps most famous for the discovery of precession, the slow change in direction of the axis of rotation of the earth. He also made estimations of the distance from the Earth to the Moon.

Ptolemy
Claudius Ptolemy, Roman astronomer, mathematician and geographer living in Alexandria, Egypt from approx. 87–150 AD established a model of the Universe based on the Greek model that would explain the motions of heavenly bodies well enough to be the standard for many centuries. Ptolemy’s model still assumed that the Earth was the center of not only the solar system, but the entire Universe—a geocentric theory. In Ptolemy’s system, everything orbits the Earth in the order Mercury, Venus, Sun, Mars, Jupiter, Saturn. For accuracy in predicting naked eye positions, it requires at least 80 epicycles, which are smaller orbit paths superimposed on the main orbits. The stars move on a celestial sphere around the planetary spheres.

From “Copernicus and the Church”
http://filer.case.edu/sjr16/pre20th_europe_church.html
Nicolaus Copernicus
Christian Church doctrine based on Greek and Roman philosophers required a solid belief in an Earth-centered Universe. The idea of a sun-centered system had been proposed by Aristarchus of Samos around 200 B.C., but arguments of Greek philosopher Aristotle prevailed, when he refuted the Sun-centered system with three questions: (1) If the Earth spun on an axis, why didn’t objects fly off?; (2) If the Earth was moving (around the sun), why didn’t it leave behind the birds flying in the air?; (3) If the Earth was orbiting the sun, why didn’t the stars appear to change their position since they were being viewed from a different perspective (the phenomenon of parallax)? This last phenomena, parallax, does occur, but is much too small to be seen without a telescope due to the extreme distance to stars. [See chapter 4.]
Planet position predictions of Ptolemaic model were getting worse and worse over the centuries. Polish astronomer Nicholas Copernicus (1473-1543 A.D.), actually a church official, favored a Sun-centered view of the Universe, yet he never publicly announced his views until he was old so as not to be branded a heretic by the Church, risking prison or even death. Copernicus’ fears were well founded, as witnessed by later notable proponents of Sun-centered systems, such as Giordano Bruno (1548–1600 A.D.) who was burnt at the stake as a heretic by the Roman Inquisition.
Copernicus recognized that a Sun-centered—heliocentric—model could easily explain certain planet movements that were serious problems for the geocentric system. He organized the five planets that were known at that time in the order that we know they are in today: Mercury, Venus, Earth, Mars, Jupiter, Saturn. The moon orbits around the Earth, he stated, but the stars are distant and don’t revolve around the sun. Since the Earth rotates around its own axis, the stars appear to revolve around the Earth in the opposite direction. Earth moving around the Sun also explained retrograde motions of the planets much more easily than the epicycles of the Ptolemaic model. Alas, Copernicus still thought that the planets move around the Sun in perfect circles, which is not actually the case, so his model still needed to have epicycles—quite a lot of them—to make accurate predictions for the motions of the planets.
Copernicus’ work, On the Revolutions of the Celestial Orbs (published in Latin: De revolutionibus orbium coelestium), was not published until the year of his death and about 73 years later (1616) the Church placed it on its Index of Prohibited Books.
“In the center of everything the sun must reside; . . . there is the place which awaits him where he can give light to all the planets.” —Copernicus
Johannes Kepler’s Laws of Planetary Motion

The problems and messiness associated with epicycles would not be overcome until Johannes Kepler (1571–1630 A.D.) came to the rescue. Kepler worked with renowned Danish astronomer, Tycho Brahe in Prague. Kepler was assigned the task by Tycho Brahe to analyze the observations that Tycho had made of Mars. Of all the planets, the predicted position of Mars had the largest errors and therefore posed the greatest problem. Tycho’s data were the best available before the invention of the telescope and the accuracy was good enough for Kepler to show that Mars’ orbit would precisely fit an ellipse. Kepler inherited Tycho’s post as Imperial Mathematician when Tycho died in 1601. In 1605 he announced his first law of planetary motion.
Kepler’s First Law:
Planets move in ellipses with the Sun at one focus.
For a circle the motion is uniform as shown above, but in order for an object along an elliptical orbit to sweep out the area at a uniform rate, the object moves quickly when the radius vector is short and the object moves slowly when the radius vector is long.
In work starting in 1602, Kepler calculated the position of the Earth in its orbit and after several years discovered that an imaginary line connecting the Sun and Earth sweeps out greater areas when the Earth is closer to the Sun, indicating Earth is moving faster in its orbit when it is closer to the Sun. Kepler stated his finding more precisely in his second law.
Kepler’s Second Law:
The planet’s radius line describes [sweeps] equal areas in equal times.
Kepler published his first two laws in 1609 in his book Astronomia Nova. It wasn’t until May 15, 1618 that he arrived at his third law.
Kepler’s Third Law:
The squares of the periodic times are to each other as the cubes of the mean distances.
This law he published in 1619 in his Harmonices Mundi. It can be stated mathematically as follows for any two planets labeled “1” and “2”:
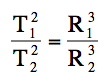
T1 = period of planet 1
T2 = period of planet 2
R1 = orbit radius of planet 1
R2 = orbit radius of planet 2
7.2 Assuming Earth’s period is 1 year and its orbit radius is about 150,000,000 km, using Kepler’s 3rd law,
(a) what is Mars’ orbit radius if it takes 687 days to orbit the Sun and
(b) how long is Jupiter’s year if its distance from the Sun is about 780,000,000 km?

Original portrait by Justus Sustermans painted in 1636.
Galileo Galilei
Italian mathematician, physicist, and astronomer, Galileo Galilei (1564–1642 A.D.) was a contemporary of Johannes Kepler and a kindred spirit, to boot. Using the newly invented telescope, Galileo discovered moons of Jupiter, mountains and craters on the Moon, phases of Venus, and sunspots. Some of these observations supported the Copernican heliocentric theory.
In 1610, Kepler heard of Galileo’s discoveries, and though they did not have any rapid means of communication, like Internet, telephones, or e-mail, Kepler published a letter of support for Galileo: Dissertatio cum Nuncio Sidereo (“Conversation with the Sidereal Messenger”). He also obtained a telescope and published his observations of Jupiter’s satellites: Narratio de Observatis Quatuor Jovis Satellitibus (“Narration about Four Satellites of Jupiter observed”). These were enormous support to Galileo, whose discoveries were doubted or denied by many.
Kepler encouraged Galileo to publish his discoveries and conclusions (see excerpts of letters on the following page), but when Galileo published papers that said that the Universe is heliocentric, he was brought before the Inquisition and accused of being a heretic (1616) for opposing the Church’s teachings. He was cleared of the charges but told to keep quiet. When Galileo published a book in 1632 that indirectly supported the heliocentric theory, he was again called before the Inquisition and found guilty of heresy, forced to recant what he had said, and sentenced to life imprisonment. Because of his age, he was placed under house arrest and continued working and experimenting until his death on January 8, 1642.
[Galileo to Kepler, 1597]
…Like you, I accepted the Copernican position several years ago and discovered from thence the causes of many natural effects which are doubtless inexplicable by the current theories. I have written up many of my reasons and refutations on the subject, but I have not dared until now to bring them into the open, being warned by the fortunes of Copernicus himself, our master, who procured immortal fame among a few but stepped down among the great crowd (for the foolish are numerous), only to be derided and dishonored. I would dare publish my thoughts if there were many like you; but, since there are not, I shall forebear….
[Kepler to Galileo, 1597]
…You advise us, by your personal example, and in discreetly veiled fashion, to retreat before the general ignorance and not to expose ourselves or heedlessly to oppose the violent attacks of the mob of scholars….
But after a tremendous task has been begun in our time, first by Copernicus and then by many very learned mathematicians, and when the assertion that the Earth moves can no longer be considered something new, would it not be much better to pull the wagon to its goal by our joint efforts, now that we have got it under way, and gradually, with powerful voices, to shout down the common herd, which really does not weigh the arguments very carefully? Thus perhaps by cleverness we may bring it to a knowledge of the truth. With your arguments you would at the same time help your comrades who endure so many unjust judgments, for they would obtain either comfort from your agreement or protection from your influential position. It is not only your Italians who cannot believe that they move if they do not feel it, but we in Germany also do not by any means endear ourselves with this idea….
Be of good cheer, Galileo, and come out publicly. If I judge correctly, there are only a few of the distinguished mathematicians of Europe who would part company with us, so great is the power of truth. If Italy seems a less favorable place for your publication, and if you look for difficulties there, perhaps Germany will allow us this freedom.
Source: Giorgio de Santillana, The Crime of Galileo (1955).
It is interesting that in light of more recent science, both Galileo and his opponents were partly right and partly wrong. Galileo was right in asserting the mobility of the earth and wrong in asserting the immobility of the sun. His opponents were right in asserting the mobility of the sun and wrong in asserting the immobility of the Earth.

Isaac Newton
If Kepler provided the most accurate descriptions of planet orbits, it was not until the work of Sir Isaac Newton (1643 -1727 A.D.) that the orbit motions would be explained in his theory of universal gravity. Newton made many other discoveries and inventions including:
- white light, when passed through a glass prism, can be seen to be made of a spectrum of colors–red, yellow, green, blue, violet
- the first reflecting telescope
- three Laws of Motion (see next page for complete description)
In 1666, Newton made the breakthrough of imagining that the Earth’s gravity extended to the Moon. Using Kepler’s third law of planetary motion, Newton deduced that there is a force (known as centripetal force) holding the Moon (or any planet) in orbit, and that force depends on distance in a certain way. If the distance is doubled, the force becomes one-fourth as much; if distance is tripled, the force becomes one-ninth as much. In general, if distance increases by a factor of “n,” the force decreases by a factor of 1/n2, a relationship known as the inverse square law. Newton also showed that Kepler’s second law (that the line joining a planet to the sun sweeps out equal areas in equal times) can be explained by the fact that a body moving in an elliptical path and attracted to one focus must indeed be drawn by a force that varies as the inverse square of the distance.
Newton ultimately concluded that this applies to all objects, and it became the Law of Universal Gravitation: Every object in the Universe attracts every other object with a force directed along the line of centers for the two objects that is proportional to the product of their masses and inversely proportional to the square of the separation between the two objects. The mathematical relation is:
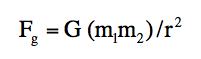
Fg is the magnitude of the gravitational force between the two objects,
G is the gravitational constant,
m1 is the mass of the first object,
m2 is the mass of the second object,
r is the distance between the objects.
The constant of proportionality G is known as the universal gravitational constant. It is termed a “universal constant” because it is thought to be the same at all places and all times and thus universally characterizes the intrinsic strength of the gravitational force.
Given the law of gravitation and the laws of motion, Newton could explain a wide range of seemingly unrelated phenomena such as
- apples falling from trees,
- cannon balls falling to the ground at some distance after being fired,
- the orbit of the Moon, planets, and the eccentric orbits of comets,
- the causes of the tides and their major variations,
- the precession of the Earth’s axis,
- the subtle change in motion of the Moon caused by Sun’s gravity.
Newton’s one system of laws of nature gave order to most of the known problems of astronomy and terrestrial physics. The work of Galileo, Copernicus, and Kepler was united and transformed into one coherent scientific theory. The new Copernican world-picture finally had a firm physical basis.
Newton’s Laws of Motion
Newton’s First Law of Motion:
Every object in a state of rest or in uniform motion tends to remain in that state unless an external force is applied to it.
Newton’s exact words were “Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.” This is often called the “Law of Inertia” and is a concept that Galileo first elucidated.
To understand Newton’s second law of motion, it’s helpful to know that
- a force is a push or pull on an object,
- an object’s speed in a particular direction is known as the object’s velocity (in other words, velocity is both speed and direction of motion), and
- a change in an object’s velocity is known as acceleration. For example, if you are in a car that goes from a speed of zero to 50 mph in 5 seconds, you and the car have experienced an acceleration of 10 mph/sec.
Newton’s Second Law of Motion:
The acceleration of an object is proportional to the force on it and is in the direction of that force.
Newton’s exact words were “The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.” Mathematically, Newton’s Second Law is often stated as follows:
If a force (F) is exerted on an object of mass (m), then the object undergoes an acceleration (a) in direct proportion to the force:
F = ma
Newton’s Third Law of Motion:
For every action there is an equal and opposite reaction.
This law is exemplified by what happens in the recoil of a gun that people so often see in TV shows and movies. When the bullet fires off in one direction, the gun recoils in the opposite direction: “an equal and opposite reaction.”

AC7.1. Investigation:
Tracking Jupiter’s Moons
Use image processing software and real telescope images to investigate and identify Jupiter’s moons; then, use the data to calculate Jupiter’s mass.
II. How Do Star-Planet Systems Form?
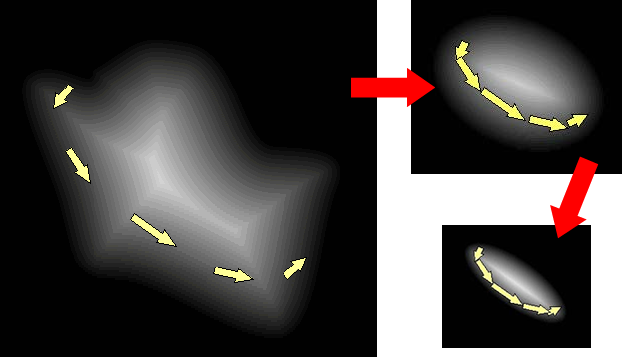
To finish the story that was begun at the beginning of Chapter 3, a nebula — a huge cloud of gas and dust in space — starts to collapse, with gravity pulling the gas and dust together. The explosion of a nearby star (a supernova), may generate shock waves in space which squeeze the cloud and trigger the collapse. Just like a dancer that spins faster as she pulls in her arms, the cloud spins faster and faster as it collapses.
At the same time, the cloud gets hotter and denser in the center and forms into a disk that gets thinner and thinner.
When the center of the cloud gets hot enough, nuclear reactions start occurring and a star, like the Sun, is born. The star not only radiates heat and light but blows its own particles outwards, pushing out remaining gas and dust of the new star system with sort of wind called a stellar wind.


III. Giant planets, rocky planets, asteroids, comets, meteoroids
Meanwhile, particles have been colliding and sometimes sticking together in clumps, eventually forming planets and moons. Two main types of planets form: smaller planets of mostly rocky material (e.g. Earth, Venus, Mercury and Mars), and large planets made of icy material and gas (e.g. Jupiter, Saturn, Uranus, and Neptune). Other icy material settles in the outer regions of the disk along with rocky material, where they form a myriad of smaller bodies.

We often refer to two types of planets, rocky planets and giant planets, but there is really a whole range of size of objects, all the way from dust grains to the giant planets. The smaller bodies are mixtures of different kinds of rock and ice—not just water ice, but other types as well, such as ammonia ice. Historically, small rocky bodies have been referred to as asteroids, while the icy bodies, that partly vaporize and form long beautiful tails when they travel to the inner parts of the solar system, are referred to as comets.
Very small bodies, either icy or rocky are called meteoroids. When a meteoroid falls into Earth’s atmosphere, it interacts with the atmosphere, heats up and leaves a streak of light in the sky that is called a meteor. If it makes it all the way to the ground, the rocky visitor from space is called a meteorite.
Studying meteorites, which are thought to be left over from this early phase of the solar system, scientists have found that the solar system is about 4.6 billion years old.



AC7.2. Investigation: Asteroid Search
Learn about a variety of current projects to find asteroids, and how you and your classmates can become involved.
The worlds come into being as follows: many bodies of all sorts and shapes move from the infinite into a great void; they come together there and produce a single whirl, in which, colliding with one another and revolving in all manner of ways, they begin to separate like to like.
—Greek philosopher (atomist), Leucippus (~480-420 B.C.)
See Staying current for this chapter.


