AC9.4. Counting Galaxies

[by Rich Lohman]

Materials:  

• One of the image processing (IP) apps listed for A Changing Cosmos on the GSS software page.
• Hubble Deep-Field (HDF) image (1995):

How many galaxies are there in the Universe?  You may have heard some numbers.  If you have (or even if you haven’t) write down a number right here that you think is the number of galaxies in the Universe.    

My guess or recollection of 
the number of galaxies in the Universe:  ________________

So how do astronomers come up with these numbers?  This activity is designed to show you an approximate way of actually counting galaxies using a real, astronomical image.  The image is called the Hubble Deep-Field image.  It was taken in December 1995 by the Hubble Space Telescope.  It wasn’t an ordinary image in many ways.  First of all, it was taken of a tiny spot in the sky near the handle of the Big Dipper.  This particular spot has no apparent objects in it that can easily be seen visually with telescopes.  Secondly, the spot in the sky was so tiny that it could be covered by a grain of sand held out at arm’s length.  Thirdly, it was an image taken over 10 consecutive days, a composite of 342 separate images.

1. Let’s take a look at the Deep-Field image.  I often call it the “Grain of Sand” image.  Open the image, “Hubble Deep-Field”, with SalsaJ.  It is in the “Images—MAST Universe” folder.  You will probably not need to adjust the Brightness & Contrast.
   
2. This is an image that calls for some appreciation.  Keep in mind how small this spot in the sky is, and that it is a very dark spot from a normal perspective.  Now for the important piece of information:  Every object you see in this image is a galaxy.  Some are reasonably nearby, but some are very far away…billions of light years!!
   
3. You will now go through an activity to “count” the galaxies in this image.  Counting all of them, however, would be a tedious job, so you’ll only be responsible for a small square in the image.  We will make the assumption (which is actually pretty good) that each square we take will be representative of the entire sky.  Here’s how we do it:
   
4. Select a square in the image:  You will use a tool called the “Rectangular Selection” tool to select a square, 100 x 100 pixels. Choose any region in the image that doesn’t include the two stars mentioned above. 
   
5. Count the objects in the square:  Now that you have a square region you simply count all the objects in that region.  It may help to zoom the image a bit (use the magnifying glass) and/or adjust the Brightness & Contrast.  Objects can be dim or bright, but all should be composed of at least a few pixels.  Keep in mind that the objects you are counting are all galaxies! 
   
   Record your number here:   ___________________  and on the white board in front.
   
6. Determine the group average for #5 above.  Use the numbers recorded on the white board from the other groups to calculate an average. 
   
   Record the group average for a 100 x 100 px. region here:  ___________
   
7. Calculate the number of galaxies in the entire image: The total size of this image is 625 x 398 px.  We’ll say 625 x 400.  If you do the math, this means 25 regions of 100 x 100 px.  So we’ll multiply the number in #6 above by 25. 
   
   Total galaxies in the Hubble Deep-Field image = _______  X 25 = ___________ galaxies
   
8. Calculate the number of galaxies in the Universe: The Hubble astronomers have calculated the size of the HDF image.  It is 0.0014 square degrees.  Keep in mind that this spot in the sky is about as big as a grain of sand held at arm’s length (or a dime placed 75 feet away!)
   
   The astronomers also tell us that there are 41,253 square degrees in the entire sky.  So the entire sky is made up of 41,253/0.0014 = 30 x 10⁶ (30 million) of these patches.  So if we multiply our number of galaxies in the entire image by 30 x 10⁶, then we should get the total number of galaxies in the Universe.
   
   A final detail in our calculation is that the Hubble Deep-Field image we are using here is only about half of the original one, so we also need to multiply by 2.  Our final result:
   
   Number of galaxies in the Universe =  Total galaxies in the Hubble image x 2 x 30 x 10⁶ 
   
     =  (from #7 above) x 2 x 30 x 10⁶ = 
   
   Number of galaxies in the Universe = _____________________
                       
     = _______________  BILLION (10⁹)!!
   
9. Comparison with the experts:  If you got between 50 and 100 billion galaxies, you’re right on track!

Distance to a Hubble Deep Field galaxy

Before estimating the distance to any Hubble Deep Field galaxy, just for fun, try answering this question about “Grain of Sand” image:

What is the angular size of a 1 mm. diameter grain of sand held at arm’s length?
[you may use the small angle formula, Angle θ = D/r x 206,265.]

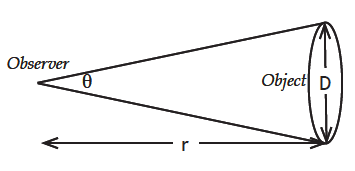
You can also estimate the distance to one of the galaxies in the image using the small angle formula, but for that you need to measure the galaxy size in pixels and then use the image plate scale to convert that pixel size to angular size. You can also make an assumption about the the size of the galaxy in light-years.

For the plate scale, you can use your answer to the question “What is the angular size of a 1 mm. diameter grain of sand held at arm’s length?”

1. Measure the number of pixels across the entire Deep Field image.
2. Calculate the Plate Scale using the Angular Size of the Grain of Sand.
3. Measure the size in pixels of one of the smaller galaxies in the image.
4. Calculate the angular size of that galaxy using the plate scale.
5. Make an estimate of the actual diameter of the galaxy you have chosen.  As a reference, the diameter of our Milky Way galaxy is 100,000 Light Years.
6. Calculate the distance to that galaxy using the small angle formula.

Is your answer in billions of light-years?