AC4. Fathoming Huge Distances

Chapter 4
I. Distance To Things in Our Solar System
For relatively nearby things, like airplanes, we can use radar waves to measure how far away they are. Radar waves are like the radio waves that radios, wi-fi, and TVs operate with.
Air traffic controllers at airports use radar systems to measure distances to airplanes. Radio waves are sent out, and they bounce off airplanes. The amount of time the wave takes to return tells the controller how far away the airplane is. The longer the time the wave takes to return, the farther away the airplane is. Radar at airports measure distances to airplanes that may be a few hundred kilometers away. Astronomical things are much farther.
The most accurate distances to the Moon, Sun, planets and other objects in the solar system are measured by timing waves sent to and from spacecraft. The speed of those waves is 300,000 kilometers per second (same as the speed of light). At that speed, it takes about one and a half seconds for the wave to get to the Moon, and another one and a half seconds to get back, so there is a distinct lag time in conversation when you’re talking by radio to someone on the Moon: nearly 3 seconds.
Rather than express huge distances in hundreds of thousands, millions, or trillions of kilometers, it’s handy to describe those distances in terms of the time it takes radio or light signals to travel that distance. A light-second is the distance that light or radio waves travel in one second. Light-second might sound like a unit of time, but don’t be confused—it’s really a unit of distance. In the case of the Moon, we could say that the Moon’s distance is about one and a half light-seconds away from Earth.
Mars is usually over 100 million kilometers away, and as Mars orbits the Sun, there are times when it is over 15 light-minutes away from us.
There would be about a half hour round-trip delay time between us and someone on Mars. Neptune, in the outer reaches of the solar system, is over 4 billion kilometers away—over 3 light-hours away.
II. Distance By Parallax
The position of an object seems to change when you change your point of view. This is the basis for another distance measuring method. Imagine that your thumb is a “star” and hold your “star’ out at arm’s length. Look at your star against the background of the other more distant things. Without moving your arm or head, look at your star first through one eye and then the other eye. Does the star seem to shift position against the background stars? The shift in position is known as parallax.
Now try holding your star closer by bending your elbow, so that the star is about half an arm’s length away. Do the same thing as before: without moving the star or your head, look at your star first through one eye and then the other eye.
Does the star’s position seem to shift less than before? The parallax shift should be greater, the closer your “star” is.

AC4.1. Investigation: Parallax
We’ll observe and measure the parallax angle of a relatively distant object, such as a tree or a flagpole, and use that angle to determine the distance to the object.
See also associated investigations:
The first people who tried to measure parallax of stars observed stars from different cities very far from each other. But they saw no shift at all. The stars were too far away for any parallax shift in position to be noticeable. They were able to measure the parallax shift for the Moon hundreds of years before radar was invented. In 150 BC, the Greek astronomer Hipparchus used parallax to measure a distance to the Moon that was only a percent different from the number we can measure today. Pretty good for someone 17 centuries before the invention of the telescope!
Measuring the parallax of the planets required much better angle-measuring techniques, and it wasn’t until 1672 that French astronomers just barely succeeded in measuring the parallax of Mars, and at last we knew how big the solar system is. The relative distances of planets from the Sun was known since the time of Johannes Kepler in 1610. So once the distance to Mars was measured, we also knew that the Sun is 150 million kilometers away from Earth!
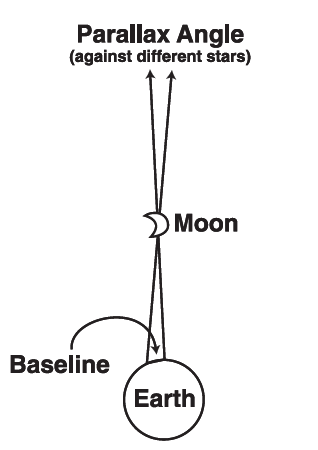
But any baseline on Earth was not long enough for making a parallax measurement to determine distances to stars.

AC4.2. Investigation:
Distance to the Moon Using Parallax
Use the app Stellarium to determine the distance to the Moon by parallax.
Distances to Stars By Parallax

After many failures in attempting to measure distance to stars by the parallax technique, a breakthrough came when astronomers realized that the fact that Earth itself changes position in space as it travels around the Sun could be employed as a very large baseline.
As the Earth travels around the Sun each year, we change our point of view by the diameter of Earth’s orbit—over 300 million kilometers! Now that’s the kind of baseline we need to see the parallax of a star. When astronomers take pictures of the same region of sky six months apart, some stars—the closest ones to us—appear to change position with respect to the more distant stars.
Astronomers tried to use parallax on the stars in the 15th, 16th, 17th, and 18th century: and they all failed. Even with the enormous baseline of the diameter of the Earth’s orbit, the parallax to the brightest (and presumably nearest) stars always came out to be 0 degrees. They were back to having to assume all the stars were infinitely far away.
Finally in 1838 Friedrich Bessel, after a year and a half of observations of one star, 61 Cygni, succeeded in measuring the parallax to a star. The parallax was less than 1/10,000 of one degree! No wonder it was so hard to measure. Bessel calculated that 61 Cygni, one of the nearest stars to us, was an incredible 25 TRILLION kilometers away. That’s 25 thousand billion kilometers!
III. Units of Huge Distance
The Light-year
A convenient unit for describing such large distances is not kilometers, or even light seconds, light minutes, or light hours, but light years. Astronomers have found that the star which makes the biggest jump every six months is Alpha Centauri. It is “only” 41 trillion kilometers away.
4.6. How many light years is the distance to Alpha Centauri?
(Hint: How many kilometers are in a light-year?)
Bessel was only off by a factor of 4; 61 Cygni is actually about 100 trillion kiliometers away.
How many light years away is 61 Cygni?
The Parsec
The technique of measuring distances to stars by parallax led to another convenient unit for expressing distance: the parsec. A parsec is the distance to an object that has a parallax angle of 1 arcsec with a baseline of 1 AU (astronomical unit, the average distance from Earth to Sun). The word “parsec”comes from a combination of “parallax” and “arcsecond.”
1 parsec (pc) ≈ 31 trillion km
≈ 3.26 light years
IV. Star Motion

Beings outside of our galaxy would see it made of billions of stars (plus assorted gases and dust) and shaped like a big spiral—a pinwheel. Might it not be spinning like a big pinwheel? Indeed it is. But for the galaxy to spin, each star must orbit the center of the galaxy. They don’t all move in perfectly synchronized orbits though, so from our vantage point stars seems to move very slowly with respect to each other. The motion has two components to it: lateral (sideways) movement and movement towards or away from us. The sideways motion is called proper motion, though no one seems to know anymore what’s proper about it. When we measure a star’s velocity towards or away from us, it’s called radial velocity (as in change of length of a radius line of a circle where we’re at the center and the star is on the circle).
V. Star Brightness and Magnitude
For really faraway stars, yet another clever distance finding method had to be found. The next trick to determine star distances was to compare their brightness.
If you observe two stars that put out the same amount of light and are equal distances away from you, the two stars appear to have the same brightness. However, if one of the stars is twice as far away from you, that star would appear much dimmer.

AC4.3. Investigation:
A Law of Brightness
A basic physics lab activity using a light sensor to measure brightness of light source(s) at various distances.
The Magnitude Scale
An ancient Greek astronomer, Hipparchus, devised a system to classify stars according to their brightness. He divided all of the stars he could see on a dark, clear night into six groups with magnitude 1 stars being the brightest group and magnitude 6 stars being the dimmest. Hipparchus did not have a telescope back in those days, so the stars he classified were only those visible to the naked eye. Astronomers still use the magnitude scale to describe the brightness of stars. Since human eyes see light in a logarithmic fashion, the mathematics of the magnitude scale is based on logs.
When astronomers considered the stars that Hipparchus must have seen when creating his magnitude scale, they found the magnitude 1 stars are about 100 times brighter than the magnitude 6 stars. In order to make this true mathematically, each change of one in magnitude must correspond to an increase in brightness by a factor of about 2.51 since 2.51 x 2.51 x 2.51 x 2.51 x 2.51 equals approximately 100. If B is brightness, m is magnitude, and subscripts a and b correspond to two stars,
mag 1 = (2.51)1 times brighter than mag 2 -or-
Ba = 2.51 x Bb when mb – ma = 1
mag 1 = (2.51)2 times brighter than mag 3 -or-
Ba = 6.30 x Bb when mb – ma = 2
mag 1 = (2.51)3 times brighter than mag 4 -or-
Ba = 15.8 x Bb when mb – ma = 3
mag 1 = (2.51)4 times brighter than mag 5 -or-
Ba = 39.7 x Bb when mb – ma = 4
mag 1 = (2.51)5 times brighter than mag 6 -or-
Ba = 99.6 x Bb when mb – ma = 5
By the same principle each half magnitude corresponds to a brightness factor of 1.6 (1.6 x 1.6 roughly equals 2.5).
Some of the brightest stars in the sky were not visible in Hipparchus’ region, so new magnitudes had to be created to accommodate them. Thus, we now have negative numbers on the magnitude scale to describe very bright objects.
When using image processing software to measure brightness of a star in a CCD image, you use the photometry tool to obtain the star’s intensity (brightness). To see the magnitude scale in terms of this intensity value, let’s assume a magnitude 0 star has brightness = 10000 (note: we are just using an arbitrary value to demonstrate the scale). Based on this brightness value, the chart (below) shows magnitudes with the associated brightness.
| Magnitude | Brightness |
| -1 | 25000 |
| 0 | 10000 |
| 1 | 4000 |
| 2 | 1600 |
| 3 | 640 |
| 4 | 256 |
| 5 | 102.4 |
| 10 | 1.0 |
| 15 | 0.01 |
The chart points out an interesting problem. The brightest star in the night sky in the Northern Hemisphere is Sirius, a magnitude -1 star. On this scale Sirius would have a brightness of 25000, which is near the upper limit of the CCD and the image processing software. In the same image, with Sirius at the upper limit of the CCD, a magnitude 15 star or even a magnitude 10 star is so dim that the software would not even identify it as a star. To see dim stars you need to choose a longer exposure time but bright stars will be overexposed.
VI. Photometry Terms
Photometry is the process of measuring the amount of light received from an object. When you display an image using image processing software, you can use the cursor to see the amount of light registered by each pixel in the image. This value is related to the number of photons striking each pixel in CCD camera.
With the photometry tools, routines add up all the values within a specific area of pixels to give the total intensity value for a star. The routines are designed to subtract background light and give only the intensity value created by the star itself. However, this is not to be confused with the magnitude brightness of the star. To avoid being confused by photometry terminology, study the definitions below.
Definitions of Photometry words
Intensity Value—The measure of light that each pixel of the CCD receives from the star. This measurement is particular to the equipment used and to the atmospheric conditions during the observation. When we display an image, the grayness or color at each pixel is based on the Intensity Value for that pixel.
Apparent Brightness—The amount of light reaching Earth per second from a star under ideal conditions (as if there were no atmosphere). This is a standard value that anyone could obtain from their measurements after correcting for observing conditions. Units of apparent brightness are watts/meter2.
Luminosity—The amount of light emitted per second by a star. It is an inherent property of the star, unlike Apparent Brightness, and is independent of where the observations were made or what telescope is used. Generally the luminosity of a star cannot be measured directly but must be inferred from other characteristics of the star. The units for luminosity are watts.
Apparent Magnitude—A measure of apparent brightness commonly used by astronomers. The magnitude scale is inverse, meaning brighter stars have lower magnitudes.
Absolute Magnitude—This quantity is analogous to the luminosity but is expressed on the magnitude scale.

AC4.4. Investigation: Star Magnitudes
Learn about the magnitude scale and compare the magnitudes of different stars.
VII. Cepheid Variable Stars as Distance Indicators
In 1784 a star in the constellation Cepheus was observed night after night by John Goodricke, and he noted that the star became brighter and then dimmer. The fluctuation in brightness repeated over and over again approximately every five days. This was the discovery of the first Cepheid variable star.
In 1908 at Harvard College Observatory, Henrietta Leavitt was examining many photographic images of the Magellanic Clouds, two small galaxies orbiting the Milky Way. She was studying the Cepheid variable stars in the Magellanic Clouds and noticed a pattern in their brightness fluctuations: the brightest Cepheids had the longest fluctuation cycles and the dimmest stars the shortest fluctuation cycles. Since the Cepheids were all in the Magellanic clouds, all at the same distance from us, comparing their apparent brightness was equivalent to comparing their luminosity.
Apparent Brightness – The amount of light reaching Earth per second from a star under ideal conditions (as if there were no atmosphere). Unit for apparent brightness: watts/meter2.
Luminosity – The amount of light emitted per second by a star. It is an inherent property of the star, independent of distance to the star. Unit for luminosity: watts.
Leavitt arrived at a general relationship between luminosity and period which she published in 1917. It is now called the period-luminosity relationship, illustrated in the diagram below and in the investigation A Cepheid Variable Star below.
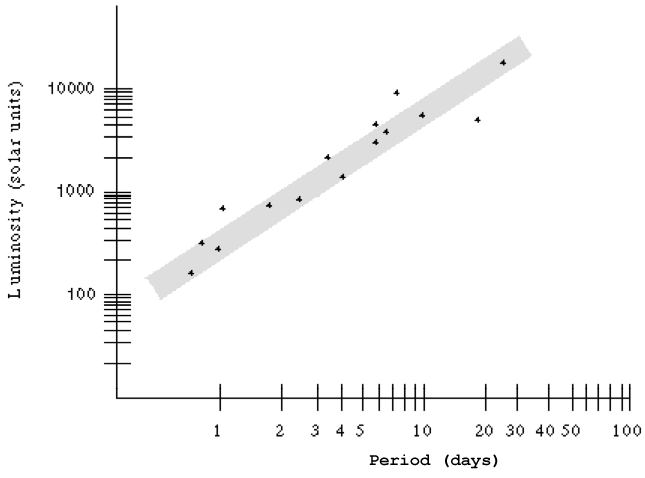
The period-luminosity diagram allows us to determine the luminosity of a Cepheid simply by measuring its period of brightness fluctuation. This is incredibly valuable for determining distance, because we can compare apparent brightness of a star with its luminosity—a comparison that hinges critically on distance. The farther away the star, the dimmer its apparent brightness is, in accord with an inverse square law. Leavitt’s discovery of the period-luminosity relationship is a milestone in astronomy. Before her research, no one had a reliable tool for measuring the distance to objects farther away than the closest stars.
To find out more about women in astronomy, see Unheard Voices, Part 2: Women in Astronomy,
A Resource Guide by Andrew Fraknoi (Foothill College)[2013-2014]
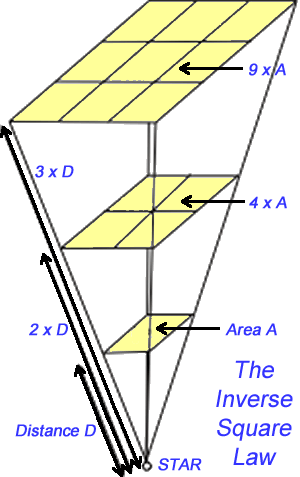
Intensity changes inversely as the distance squared.
The mathematical relationship is known as the inverse square law.
The technique for determining the distance of a Cepheid requires three basic steps:
- Measure the period of fluctuation and infer the luminosity of the Cepheid.
- Use a standard star to calibrate the image and determine the Cepheid’s apparent brightness.
To measure the period of fluctuation, the Cepheid must be observed at least every few nights for several weeks. The light intensity measured for a Cepheid will change from night to night for two reasons:
- the changing observing conditions and
- the changing luminosity of the star.
In order to get a plot of the Cepheid’s changing luminosity you must remove the effects of the atmosphere by including a reference star. Since the Cepheid star and the reference star are on the same image, the observing conditions are the same for both stars. If the observing conditions did not change from night to night, the reference star would appear just as bright each night. In general, observing conditions do change, so the number of Counts measured for the reference star will increase or decrease depending on how much light the atmosphere lets through. If the atmosphere blocks out a large amount of light on one night, both stars will appear dimmer; on a clear night, both stars will appear brighter.
If the Cepheid had constant luminosity, the ratio of Counts between the Cepheid and the reference star would remain constant. A Cepheid is not constant, however. As the luminosity of the Cepheid increases because of internal changes in the star, the ratio of Counts measured for the Cepheid to the Counts measured for the reference star will increase. By measuring this ratio for each image, you can plot the true brightness fluctuation of the Cepheid.

AC4.5. Investigation:
A Cepheid Variable Star
Plot the light curve for a cepheid, then find its luminosity and distance from our solar system.
We’ll find out more about uses of Cepheid variable stars in Chapter 9, The Universe Begins … and Ends?
The observations of the Cepheid were made through a Visible (V) filter. This filter blocks out almost all light except in the yellow-green part of the color spectrum. When you calculate the luminosity and apparent brightness of the Cepheid you must remember that these only refer to the amount of light coming through the V filter. This is fine for your measurements because you can compare them to other measurements taken through the same kind of filter. However, it is not valid to compare these values to the apparent brightness or luminosity of a star over all wavelengths. In this unit, all measurements are through the V filter.
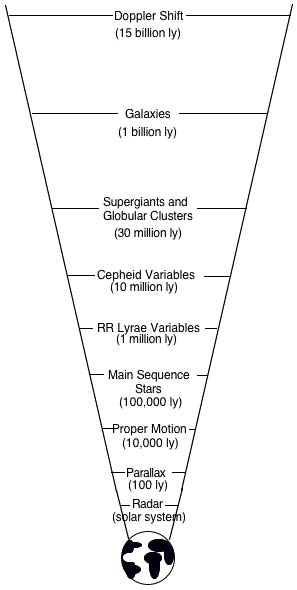
Techniques of Distance Finding: The Cosmic Distance Ladder