AC4.2. Distance to the Moon Using Parallax
Overview: We’ll observe and measure the parallax angle of a relatively distant object, such as a tree or a flagpole, and use that angle to determine the distance to the object.
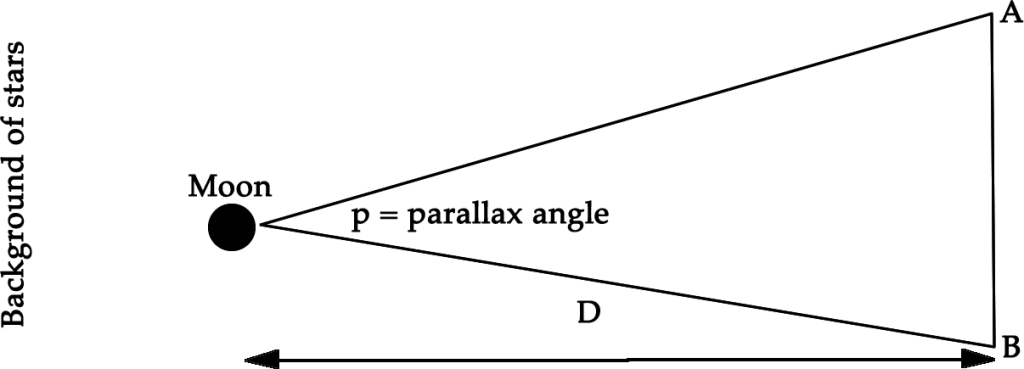
Geometrically, parallax shift for the Moon can be represented by this diagram:
Points A and B are the two viewpoints. Length AB is called the baseline. The position of the moon against the background of stars will be different from points A and B. That difference can be measured in terms of an angle, p, the parallax angle. D is the distance from the baseline to the Moon. Mathematically the diagram can be represented by the following equation:Angle p = (AB/D) radians = (AB/D) x (180/π)
Rearranged: D = (AB/p) x (180/π)
[p in degrees; D in the same units as AB]
Therefore, in order to determine the distance to an object using parallax we need to view the object from two different points of view. Then we need to determine the length of the baseline and measure the parallax angle.
In this activity we will use Stellarium to view the moon from two different locations on the Earth. We will use two positions on or very close to the equator. This will make the calculation of the point to point baseline much simpler. The two locations will be Quito, Ecuador, and Nairobi, Kenya. Stellarium will allow us to measure the parallax angle.
- Open Stellarium and set the location for Quito, Ecuador. Keep the Location Window open.
- Record the Longitude and Latitude of Quito from the Location Window:
Long = __________________, Lat = ____________________ - Set the date and time for July 15, 2011 and 18:00 hours.
- Do a Search for the Moon if it is not in your view.
NOTICE that it sits just on the edge (almost touching the line) of the constellation Capricornus.
The Moon should also be very near the Eastern horizon, just after it has risen.**
**This may not be true because of an issue between your computer clock and the local time in Ecuador. If not, either increase or decrease the HOUR on your Date/Time window so that the full moon is very near the eastern horizon. The actual time in Ecuador may be very different from what the Date/Time Window reads!! - Click on the Moon and read its RA/Dec (of date) for Quito in the upper left corner:
RA = ….__________________ Dec = ____________________ - Now set the location for Nairobi, Kenya, but keep the Location Window open.
The TIME stays the same. - Record the Longitude and Latitude of Nairobi from the Location Window:
Long = __________________, Lat = ____________________ - Search for the Moon if it’s not in the view.
Once again it should be near Capricornus,
but NOTICE that it is a bit farther away from it than when viewed from Quito.
You are seeing parallax “in action”.
The Moon is much closer to the Earth than any of the stars that make up the constellations,
so you see it in slightly different positions depending upon your viewpoint on the Earth. - Click on the Moon and read its RA/Dec (of date) for Nairobi:
RA = ….__________________ Dec = ____________________
We now have enough data to calculate the parallax angle and the baseline. Since we are viewing the moon from points on approximately the same latitude (the equator), the parallax angle is simply the difference in the RA of the two positions.
p = parallax angle = RA (Quito) – RA (Nairobi) =
The result will be in minutes of RA.
Since 1 hour of RA = 15 degrees of angle, 1 minute of RA = 15/60 or 0.25 degrees of angle.
You do the math to get the parallax angle in degrees.
p = _________ degrees.
Now for the baseline: Once again we know that both Quito and Nairobi are on (or very close to) the equator. That simplifies the geometry a bit.
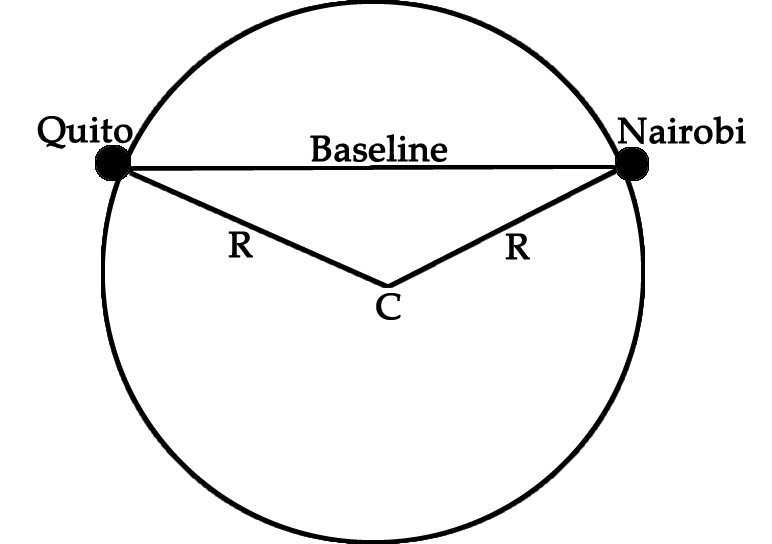
This diagram helps:
The circle represents the equator of the earth when viewed from the north pole down.
Quito and Nairobi lie on two points along the equator.
R is the radius of the earth equal to 6400 km.
The angle at C can be computed from the longitudes of the two cities.
In fact it is just the sum of the two longitudes, since one is West and the other East.
Angle C = Longitude of Quito + the Longitude of Nairobi
= _______________ + _____________ = ___________ degrees.
Once that is determined one can use the Law of Cosines to calculate the baseline:
(Baseline)2 = R2 + R2 – 2R2 x cosC
(Baseline)2 = 64002 + 64002 – 2(6400)2 x cosC
The result:
Baseline = __________________ km.
Finally we can calculate the Distance to the Moon using the equation from earlier:
D = (AB/p) x (180/π) [AB = baseline; p = parallax angle]
D = __________________ km.
Compare this result to the published average value of about 384,000 km.***
***Note that this number is the average distance from the center of the Earth to the moon. We have calculated the distance from the baseline to the Moon. The difference is not great, but on the order of 3400 km. in this case.


