AC4.1. Parallax
There are also 4 other investigations associated with this investigation:
- Indoor activity: Parallax—How Far Is It?
- Distance to Asteroid 1998wt
- Parallax of Asteroid Austria
- Parallax of Asteroids using JS9(AiM): Worksheet 1 – Worksheet 2
- See also Parallax slide set (from Rich Lohman)
Overview: To see how parallax works, we’ll observe and measure the parallax angle of a relatively distant object such as a tree or a flagpole and use that angle to determine the distance to the object.
Materials
Ruler, meter stick, Parallax Diagram.
n
Parallax Diagram
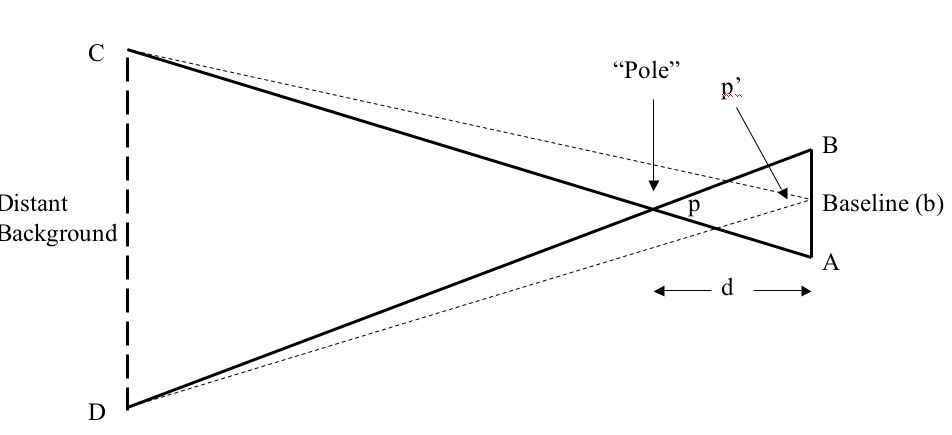
Refer to the Parallax Diagram for these steps:
I. Locate a target object, like a pole or tree, whose parallax and distance you want to measure.
4.1 Make an estimate of the distance to the target object in meters, and record your estimate. This will allow you to appreciate how well you can visualize distances that are beyond your reach. It will also help in determining whether your result at the end is reasonable or not.
II. Find an area where you can lay out a baseline about 10 meters long with these qualities:
- (a) you can sight the target at approximately either end of the baseline, points A and B on the diagram,
- (b) from near point A you can sight on the target and line up an easily seen object in the far distance, preferably a few miles or more behind the target, point C, and
- (c) from the other end of the baseline, near point B, you can line up the target with another, easily seen object in the far distance, point D.
III. Mark positions A and B and measure the baseline distance (b) between A and B in meters. It should be in the range of 5–10 meters. Record that distance on the diagram (letter b).
4.2. Measure the parallax angle of the target by standing somewhere along the baseline where you can view both points C and D in the distance. The closer you are to the center of the baseline, the better, but any point along the baseline will work. With the help of a partner, measure the angle between points C and D (angle p’ on the diagram), as follows:
- a. Hold the ruler in front of your eye and measure the distance (x) between C and D.
- b. At the same time have a partner with a meter stick measure the distance (y) from your eye to the ruler you are holding. Have more than one pair of people do this measurement for the most reliable result.
- c. Compute the parallax angle: p’ = (x/y) * 57.3 degrees*.
4.3. Calculate the distance, d, to the pole. Assume the angle is fairly small, so you can use the following approximation:
d = b (57.3°/ p’)
Refer to the Parallax Diagram for these steps:
I. Locate a target object, like a pole or tree, whose parallax and distance you want to measure.
4.1 Make an estimate of the distance to the target object in meters, and record your estimate. This will allow you to appreciate how well you can visualize distances that are beyond your reach. It will also help in determining whether your result at the end is reasonable or not.
II. Find an area where you can lay out a baseline about 10 meters long with these qualities:
- (a) you can sight the target at approximately either end of the baseline, points A and B on the diagram,
- (b) from near point A you can sight on the target and line up an easily seen object in the far distance, preferably a few miles or more behind the target, point C, and
- (c) from the other end of the baseline, near point B, you can line up the target with another, easily seen object in the far distance, point D.
III. Mark positions A and B and measure the baseline distance (b) between A and B in meters. It should be in the range of 5–10 meters. Record that distance on the diagram (letter b).
4.2. Measure the parallax angle of the target by standing somewhere along the baseline where you can view both points C and D in the distance. The closer you are to the center of the baseline, the better, but any point along the baseline will work. With the help of a partner, measure the angle between points C and D (angle p’ on the diagram), as follows:
a. Hold the ruler in front of your eye and measure the distance (x) between C and D.
b. At the same time have a partner with a meter stick measure the distance (y) from your eye to the ruler you are holding. Have more than one pair of people do this measurement for the most reliable result.
c. Compute the parallax angle: p’ = (x/y) * 57.3 degrees*.
4.3. Calculate the distance, d, to the pole. Assume the angle is fairly small, so you can use the following approximation:
d = b (57.3°/ p’)
Note: 57.3 is the approximate number of degrees in a radian which is another unit of angle. A more accurate value is found by dividing 180 by “pi”. A radian is the angle along the circumference of a circle made by a length equal to the radius of the circle.
4.4. Compare your measured distance to the value you estimated in question 4.2 above. Do you believe your measured result is reasonable? Explain.
4.5. Which step of the procedure do you believe had the most potential for error? Without doing a major error analysis, approximately what percent error do you feel there is in your result of distance to the pole?
Investigations on Measuring Distances to Asteroids
There are two investigations (by Rich Lohman) on using the parallax technique to find distance to asteroids:
Images for the investigation Distance to Asteroid 1998wt are in the folder “MoreTelescopeImages/AsteroidParallax” available on the HOU/GSS software download page.
The measurements for angles in telescopes are usually not in units of degrees, but arcminutes or even arcseconds. As with the units of time, there are 60 arcminutes (‘) in a degree and 60 arcseconds (“) in an arcminute. The equation in step 4.3 above has the constant 57.3° (the number of degrees in a radian). If your measurements are made in arcseconds instead of degrees, then the constant to use would be 57.3° * 60 arcmin/° * 60 arcsec/arcmin = 206,265”. So the equation to use becomes
4.4. Compare your measured distance to the value you estimated in question 4.2 above. Do you believe your measured result is reasonable? Explain.
4.5. Which step of the procedure do you believe had the most potential for error? Without doing a major error analysis, approximately what percent error do you feel there is in your result of distance to the pole?
* 57.3 is the approximate number of degrees in a radian which is another unit of angle. A more accurate value is found by dividing 180 by “pi”. A radian is the angle along the circumference of a circle made by a length equal to the radius of the circle.
Investigations on Measuring Distances to Asteroids
There are two investigations (by Rich Lohman) on using the parallax technique to find distance to asteroids:
Images for the investigation Distance to Asteroid 1998wt are in the folder “MoreTelescopeImages/AsteroidParallax” available on the HOU/GSS software download page.
The measurements for angles in telescopes are usually not in units of degrees, but arcminutes or even arcseconds. As with the units of time, there are 60 arcminutes (‘) in a degree and 60 arcseconds (“) in an arcminute. The equation in step 4.3 above has the constant 57.3° (the number of degrees in a radian). If your measurements are made in arcseconds instead of degrees, then the constant to use would be 57.3° * 60 arcmin/° * 60 arcsec/arcmin = 206,265”. So the equation to use becomes
d = (b/p”) x 206,265 .
where
d = distance to asteroid.
b = baseline.
p” = parallax angle (arcseconds).


