AC3.2. Plate Scale of a Smartphone

Investigation 3.2
Materials
One of the image processing (IP) apps listed for A Changing Cosmos on the GSS software page.
Steps
I. In order to look at “Smartphone” images with SalsaJ or JS9, you need to be able to transfer photos from your smartphone to your computer and know where to find those images on your computer:
- Using your smartphone, take one or two photos of anything or anyone.
- Using an appropriate cable, email or text message, transfer the photo(s) from your smartphone to a computer that has the SalsaJ software or that can connect to JS9 online.
- Locate where the image(s) are on your computer and copy one of these files to your desktop. On some Windows machines, they may appear in the folder “My Computer” > “Smartphone” > “DCIM”.
- Open SalsaJ. Click the “File” menu and locate and open the photo on the desktop menu. For JS9, see JS9 Manual by Mr. Robert Curtiss, Science Teacher and Quiz Bowl Coach, Theodore Roosevelt High School, Wyandotte, Michigan.
- Use the “zoom” tool until you see the pixels of the picture.
II. Steps to calibrate the camera/smartphone
and calculate its Plate Scale
- Get a balloon for your group and inflate it to a diameter of 15 cm., approximately.
Measure the diameter and enter it here.
D = ______________ - Take a picture of the balloon at a distance of about 2 meters, and measure that distance with a meter stick.
Enter it here.
r1 = ___________ - Take another picture of the balloon at a greater distance (about 2x the first).
- Measure that distance and enter it here.
r2 = ___________ - Using image processing app/software to open the file for the first picture.
- Zoom the photo until you can see the pixels of the balloon.
- Use the tools “Straight line selection” and “Plot profile” to measure the diameter of the balloon in pixels.
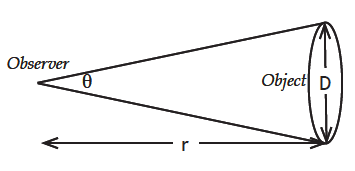
Enter it here. ___________________ - Now you need to calculate the angular size of the balloon at the first distance. Use the small angle formula for calculation. Do it here:
Angle A = (D/r1) x 57.3 degrees = ______________
Angular size = _______
- Now that you have the angular size and the pixels of the balloon you can calculate the Plate Scale. This is done by dividing the angle by the pixels. The result has units of degrees per pixel, or it can be changed to arcminutes per pixel. Perform the calculation here:
Plate Scale = Angular size/Pixels = _______________
Plate Scale = __________ - You can now use this “Scale” for any picture using this camera. Use it to calculate the angular size of the balloon in the second picture. First determine the pixels of the balloon in the photo, and then calculate the angle using the scale plate.
Angular size = Plate Scale x Pixels
= ______ x _________ = ___________ - Finally you can use the formula, Angle A = (D / r) x 57.3 degrees, to calculate the distance to the balloon in the second picture. Using a little algebra gives:
r = (D / A) x 57.3 = (__________ / __________) x 57.3 =
The result, r, has the same units as D. Convert r to meters and compare your result to the distance you measured for the second photo.
Plate scales for telescopes
The focal length (F) of a telescope is the distance over which light rays are brought from the primary lens or mirror to the focus point near where the eyepiece or camera is positioned. If the focal length of a telescope is known, its plate scale is very simple to compute:
Plate Scale = 1/F.
This gives the plate scale in units of radians/mm if the focal length is in millimeters.
However, a more convenient unit for plate scale is (seconds of arc)/mm or “/mm and for that, the radians must be converted to seconds of arc. Since there are 206,265 “/radian,
Plate Scale = 206,265/F (unit is “/mm)
Often the exact focal length of the optical system in a telescope is not known. In that event, one can identify at least two well defined reference targets in the image—objects where the positions (RA and Dec) are known accurately. From the RA & Dec coordinates, the angular spacing of the objects can be determined and then divided by their distance apart on the CCD to compute plate scale.

