EU5.1. Energy and Power

{ Energy Use Contents } { All GSS Books }

You are browsing in a store to buy a light bulb to replace a burnt-out bulb. Will a 60-watt bulb be bright enough? Were you satisfied with its brightness? How about a 75-watt bulb? Why not a 100-watt bulb? What is a watt anyway? Watts are units used as a measurement of power. Here is the scientific definition.
Power is the rate at which work is being done.
Another way to think of it:
Power is the rate at which energy is being transformed.
The 100-watt bulb is brighter than a 60-watt bulb because it transforms more electrical energy to light energy in a given amount of time.
Using P for power, W for work, T for the time during which the work is being done, the equation for power is:
P = W/T
Power is measured with different kinds of units, depending on the type of energy that is being transformed. Watts can describe any power use, but it is most often used for electric power. Fuel burning engines and large electric motors are often rated in units of horsepower. Until the 20th century much of the heavy work in the world was done by horses and other animals, so it was natural to think of energy use in terms of the work a horse could do.
Questions:
5.2 Can you think of instances in the United States, and around the world, where animals are still used for their power?
5.3 How many 100-watt light bulbs would have the power equivalent of a 40-horsepower car? (One horsepower is 746 watts.)
5.4 What power did a newlywed husband have to generate to lift his new bride the distance of one meter in one second? The bride weighs 500 newtons and suppose 1 newton = .22 pounds.
5.5 Remember the problem on page 19: If an automobile has expended an amount of energy equivalent to 1,200,000 joules of work, and to propel the car the engine is exerting a force of 600 newtons, how far has the automobile traveled? Now, if it took the automobile two minutes to travel that distance, what was the power of the automobile?
Sample Problem
How much power does it take to lift a book from the floor to a shelf at a height of two meters in two seconds, if the book weighs the equivalent of 0.25 newtons?
Solution:
P = W / T
W = 0.5 joule (see page 19)
T = 2 seconds
P = 0.5 joule / 2 seconds = 0.25 joule/seconds = 0.25 watt
A unit of work common in science is a joule. One joule is equivalent to the work needed to move an object a distance of one meter while applying a force of one newton. If you work at a rate of one joule every second, you are expending power at a rate of 1 watt. In other words, 1 joule/second = 1 watt
Volt and Amps

The power of Niagara Falls depends on two factors: the sheer height of the falls, and the vast current of water in the Niagara River. If the current of water were no more than a trickle it wouldn’t have much power at all, no matter what height it fell from. If the height of the falls were just an inch or two it wouldn’t have enough power to turn even one turbine. The height of the water relates to its potential energy. The current of water converts that potential energy to kinetic energy as the water drops.
The power of electricity can be compared to the power of running water. Imagine the tremendous power of a large waterfall like Niagara Falls. Its power can turn a dozen huge electrical generators at once.
In a wire that carries electric power there is a current, but it is not a current of water. It is a current of electric charge. Like water, electric charge can flow in a current. The flow of electric current is measured in amperes (often called amps).
Like water, electric charge can have potential energy. The potential of electric charge is measured in volts. The voltage of a typical flashlight battery is 1.5 volts. Put two of those flashlight batteries together end to end and you have 3 volts. The electric charge that flows around a 3-volt circuit does twice as much work, or transforms twice as much energy as the electric charge in a 1.5 volt circuit.
Most electric appliances are designed to run only at a particular voltage. Standard outlets in the United States are kept at 110V to 120V. Some high-power appliances, such as electric clothes dryers, run on 220V.
Question 5.6
Is there a 220V outlet where you live? In which room?
For what appliance(s)?
Electrical Energy & Electrical Power
These two flashlights operate at different voltages. Can you tell which one is more powerful? The one with two batteries, right? Not necessarily. Voltage is only half the story. The power depends on the voltage and the current, just like the power of Niagara Falls depends on both the current and height from which the water falls.
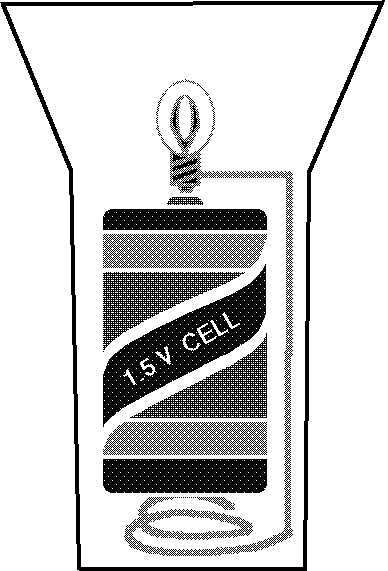
In the simple circuits of a flashlight, electric current makes a trip from one end of the battery (or batteries) to the other end. The voltage of the battery determines how much work each bit of electric charge does along the way, just as the height of a waterfall determines how much energy is converted as each gallon of water drops to the bottom.
The power, P, of any electrical device, is the product of the voltage, V, and the current, I.
P = V x I
For any appliance, if you know the current (in amps) and the voltage (in volts), you can use this formula to find its power in watts —even if its wattage is not listed on the label. Find the missing values in the table below:
An electric company does not charge for power. It charges for energy. Can a 40-watt lamp use more energy than a 1000-watt hair dryer? Yes, if the hair dryer is on for five minutes a day and the light bulb is left on all night.
The energy, E, an appliance uses is its wattage, P, times the amount of time, T, that it is turned on.
E = P x T
If the power is in watts and the time is in hours this formula gives you the energy in watt-hours. A 100-watt light bulb shining for one hour will use 100 watt-hours of energy. During a typical month a household uses thousands of watt-hours of electricity so an electricity bill generally lists electricity use in kilowatt-hours.
1 kilowatt-hour = 1,000 watt-hours = 3,600,000 joules
Question 5.7.
What values would go in the blank cells of the table below?
| APPLIANCE | VOLTAGE | CURRENT | POWER |
|---|---|---|---|
| Laser printer | 115 volts | 7 amperes | ??? |
| Digital clock | 120 volts | ??? | 5 watts |
| Food Processor | ??? | 6 amperes | 690 watts |
| Heating pad | 120 volts | 0.4 amperes | ??? |
| Hair dryer | 120 volts | 12.5 amps | ??? |
Electrical Conductors and
Electrical Resistance
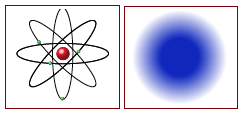
Two Ways to Picture an Atom
In an atom, positively charged protons and neutrons are bound together in the nucleus at the center. Negatively charged electrons occupy the rest of the space in the atom. The “planetary” model is often used to illustrate an atom (left). The size of the nucleus is drawn a hundred thousand times larger than it is. In modern physics we realize the exact position and path of an electron can never be known, so electrons may be depicted as a kind of cloud around the nucleus (right). In this drawing, the electron cloud of a helium atom is enlarged about one hundred million times. At this scale the nucleus is an unprintable small dot.

In many materials all the electrons in each atom are bound tightly to the nucleus. Such materials are called insulators—they do not allow electricity to flow easily. Glass, rubber, and plastic are good insulators. Materials that are good conductors of electricity have electrons that are not bound to any particular atom. The electrons flow easily among the atoms in the solid. Silver is the best conductor, but copper and aluminum are used more often in wiring.
Can you guess why?
In a conductor, as electrons flow, they bump into atoms, causing them to jiggle and heat up the conductor. This effect is called resistance. Resistance transforms electrical energy into heat energy. In your home, there is a limit to how much current the wires can safely carry without danger of overheating and causing fires. Circuit breakers and fuses are devices that switch off the electricity if the current rises above a safe level.
Measuring Resistance
Electrical resistance is measured in ohms. The amount of resistance, R, in ohms, is defined in terms of the voltage, V, and current, I, by the formula:
R = V / I
This is known as Ohm’s Law. Example: If you double the voltage across a wire, the current through the wire will double.
Units to use in the formula:
- Resistance R is in ohms
- Voltage V is in volts
- Current I is in amperes
Sample Problem
A home toaster is rated to operate with an electric current of six amperes on a 120 volt electric line.
What is the resistance of the toaster’s heating elements?
Solution: R = V / I = 120 volts / 6 amperes = 20 ohms
Question 5.8
What are the resistances of these appliances?
A laser printer for a computer: 115 volts; 7 amps
Digital alarm clock: 120 volts; .04 ampere (40 milliamperes)
Food processor: 115 volts; 6 amperes
Heating pad: 120 volts; 0.4 amperes
Hair dryer: 120 volts; 12.5 amperes
Power Losses in Transmission Lines

The high voltage transmission lines used to get electric power from the power plant to the neighborhoods where the electricity is used are necessary to minimize losses of energy in the wires due to the wires’ electrical resistance. For a wire of resistance R, with a current I flowing through it, the power loss PLost can be calculated by this formula:
PLost = I2 x R
Units to use in the formula:
- Resistance R is in ohms
- Power P is in watts
- Current I is in amperes
Mnemonic: Twinkle, twinkle, little star. Power equals I squared R.
The less current that flows, the less power is lost. So how can an electric company deliver high power with less current? Remember that power is voltage times current, so the same power can be delivered using low current at high voltage or high current at low voltage. Which alternative gives the least power loss from resistance in the wires? From the power loss formula above, the answer is obvious: minimize the current and maximize the voltage.
Sample Problem
In the problem of the home toaster on page 53, what was the power given off as heat in the toaster’s heating elements?
Solution: The toaster’s current use was six amperes and we calculated the resistance to be 20 ohms. PLost = I 2 x R = (6 amperes)2 x 20 ohms = 720 watts
Question 5.9
Standard long distance power lines carry electricity at 230,000 volts. Suppose the resistance in a particular stretch of power transmission line is 100,000 ohms and current is flowing at 0.1 ampere. What is the power loss in the transmission line?
Question 5.10
Some long distance power lines operate at 765,000 volts.
How much less power would be lost in a 100,000 ohm line operating with a current of .03 ampere at 765,000 volts as compared with .1 ampere at 230,000 volts?
Superconductors–No Resistance
In 1911, H. Kamerlingh-Onnes assigned his student assistants to find out how the electrical resistance of metals changed when they became very cold. When the students reported that some materials had absolutely no resistance at extremely cold temperatures he sent them back to figure out what mistake they had made. There was no mistake. They had discovered superconductors.
Superconductors have been used in devices such as experimental computers and medical equipment. Using superconductors in long distance power lines, electromagnets, or motors might be a way to save energy if it were not for the problem of refrigeration. Keeping superconductors cold enough uses energy. Researchers have made many breakthroughs in superconducting technology but scientists still do not fully understand how they work. Further research may show ways to save energy with these materials.

